Yesterday, the Telegraph published an article by Dan Hodges accusing UK pollsters of herding. For those unfamiliar with the term, herding is the unnatural convergence of results between polling companies, sometimes seen as an election approaches. Various cases have been documented in the US – the more egregious ones involve pollsters deliberately manipulating their numbers.
But herding can also take more subtle forms. Pollsters have a number of methodological decisions to make in order to achieve a sample representative of the population – phone or online fieldwork, which variables to weight by, which parties to prompt for, how to model turnout, how to handle don’t knows and refusers, and so on. In many cases there is no “right” or “wrong” answer, but these decisions have consequences for the final results. If pollsters systematically err on the side of the herd when picking a methodological path, polls will end up with unnaturally similar results.
So is there evidence that herding happened in Britain? I’ve replicated – as closely as possible -the Nate Silver analysis that Hodges refrenced, based on the Labour-Conservative spread, and taking absolute differences to its 21-day rolling average. I’ve done it in two versions – one for all regular pollsters and a second that excludes YouGov, due to the very high frequency of their polls giving them a correspondingly outsize weighting in the version that includes them:

You can see from the chart that polls didn’t suddenly fall into line as election day approached. The shape of the LOESS trendline looks nothing like the “herding” one in Nate Silver’s piece – it looks much more like the one in the “gold standard” chart (the second one) in this piece by his colleague Harry Enten. (Incidentally, this chart does highlight a genuine problem – the reaction to outliers. If I weighted the polls by column inches and airtime they received, it would look rather different…)
There are legitimate reasons why polls might converge. To give just a couple of examples, as don’t knows make their minds up, the impact of some pollsters excluding them while others reallocate them in various way becomes smaller. And at the very end of the campaign, pollsters often increase their sample sizes, reducing (sometimes considerably) the variability inherent in sampling. I wrote about how house effects were relatively small in October and Anthony Wells did so in January. There have been periods of temporarily increased divergence, and in particular between phone and online polls, but not in a way that looks suspicious.
But why are the trendlines lower (implying smaller errors) than in the US races that FiveThirtyEight analysed? There are two main reasons. Firstly, sample sizes are typically larger in Great Britain-wide polls than in US Senate polls of a single state (headline sample sizes of 2,000 are now standard online and sub-1,000 in any mode is now very rare).
The second reason is more technical. The “theoretical minimum” average error that Silver calculates is based on the standard error (from which the margin of error is also derived) of the spread between the Democrat and the Republican. When there is no-one else in the race, the correlation between the two is basically assumed to be perfectly negative (US polls tend to include don’t knows in their headline numbers, but for this purpose their impact is small). This means that the statistical error on the lead is basically double the error on one of the parties.
But in Britain’s multiparty environment, things are different. Labour and Conservative vote shares are not perfectly negatively correlated. Case in point – from the start of 2015, both gained at the expense of smaller parties. Therefore the standard error on the lead is quite a bit less than double the error on the share (by how much is tricky to calculate for the same reason).
But what about the pattern of polling errors in finals polls? I’ve devised an exercise to examine just that, for each party. Firstly I’ve taken the taken the polling error of each pollster and subtracted the average error across all 11 pollsters in this table. Then I’ve calculated the standard error for each observation, taking into account the vote share of the party in question and the effective sample size in each poll. The actual error is then expressed as a multiple of the standard error, giving the normalised error.
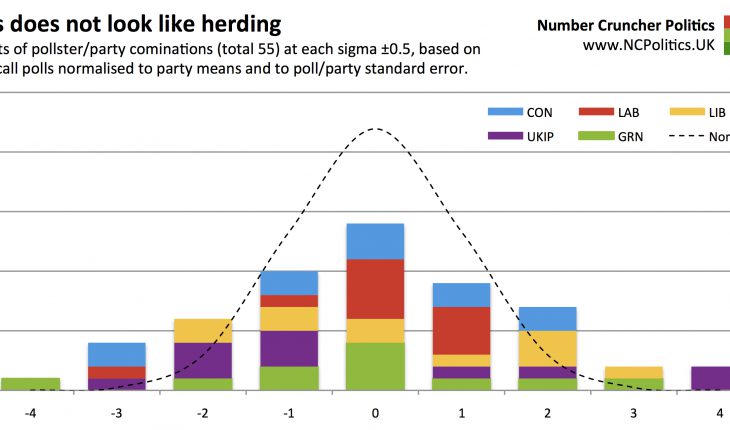
In the following bar charts, each “block” is an instance of one final call poll having a normalised error at each (rounded) number of sigmas above or below the mean (zero). The dotted line is the distribution we’d theoretically expect given true random samples (and apologies to pedants for the fact that the profile is mildly distorted between sigma points – due to an apparent limitation in Excel – but at the round numbers its level is correct). And since you can’t have half a pollster, the bar chart pattern is inevitably a bit “lumpy”.
If pollsters were herding, there would be too many of them in the middle of the chart and too few at the wings. But for the Conservative vote share, we see the opposite:

For Labour, it’s less clear cut at first glance. We’d expect four or five pollsters to be bang in the middle and there are five. There are too many at +1 and too few at -1. But across these three points we find 10 pollsters, the closest whole number to the 9.7 that you’d statistically expect:

Now let’s combine all five GB-wide parties (55 observations in total) into one chart. For those interested, the individual charts are available at the following links for the Lib Dems, Greens and UKIP. If there’s one chart that tells the story, this is it. The distribution is flatter than implied by theory:

This is what you’d expect – the theoretical estimate assumes pure random samples which (as recent events may have demonstrated) is not the case, so the observed errors will vary more. These results have a standard deviation of about 1.8, and a fair amount of excess kurtosis (fat tails). In short, no sign of anything dodgy.
None of this guarantees that there weren’t isolated cases of individual pollsters herding. But the polling failure was an industry-wide problem, and the evidence doesn’t support the idea that herding was a cause.
Is there evidence of pollsters herding?
|
25th June 2015 |